【结构化学】第二章原子的结构与性质

type

status

date

slug

summary

2.1 单电子原子的薛定谔方程及其解

我们在求解单电子原子如H原子、和等粒子时，得到薛定谔方程为

[什么是折合质量？]

当我们研究两个相互作用的质点组成的系统的运动时（如A和B），两个物体都在动，研究起来比较麻烦。为了简化，尝试将一个物体（A）视为静止，只观察另一物体（B）的运动。在新的参考系下，B的质量为折合质量

证明如下：

对于物体A

对于物体B

当把A看做静止时，B相对A的加速度为

由牛顿第三定律得

通过这个转化我们就将二体问题转化为以A为参考系，物体B运动的单体问题。新的体系下物体B的加速度为，质量为

当我们研究氢原子中电子的波函数时，本质是在研究原子核和电子之间的一个二体运动，为了简化运算，将电子的质量换算为了折合质量。

观察薛定谔方程，发现势能项里存在变量半径，为了方便计算，采用Laplace算符的球坐标形式

带入薛定谔方程整理得

令，带入薛定谔方程整理得到三个常微分方程：R方程，方程和方程，用解常微分方程的方法，求得3个方程满足的品优条件的解，乘在一起得

其中方程比较好解，为常系数二阶齐次线性方程

根据归一化条件以及得到复数形式的解为

复数形式的对角动量沿z轴分量的算符，是本征函数，但复数不容易画图。

根据态叠加原理，将两个特解进行线性组合仍是的解，将其线性组合可得到实函数解

但实函数解对角动量沿z轴分量的算符不是本征函数，但便于作图。

注：复函数解和实函数解不是一一对应关系，而是线性组合关系。

对于得到的称为原子轨道函数，简称原子轨道，其中n（主量子数），l（角量子数），m（磁量子数）

其中称为波函数的径向部分，称为波函数的角度部分，是个球谐函数。

2.2 量子数的物理意义

主量子数n

在解方程时，得到

即n决定了体系能量的高低，相邻两能级差随n增大逐渐减小

零点能效应：受一定势场束缚的的微观粒子在能量最低的基态时仍然在运动。

问题：氢原子基态时总能量，动能是多少? 势能又是多少? 动能和势能的占比是怎么分配的呢?

位力定理：对势能服从规律的体系，平均势能和平均动能满足：

位力定理的证明：https://zhuanlan.zhihu.com/p/138874889

原子核和电子之间为库伦作用，势能为规律

所以

联立

得

角量子数l

单电子原子的轨道波函数对角动量平方算符是本征函数

所以

即决定了电子轨道角动量，被称为（轨道）角量子数

带电粒子有了角动量就会有磁矩，磁矩与角动量的关系为

磁量子数m

单电子原子的轨道波函数对角动量在z方向的分量算符是本征函数

所以

同理，单电子原子的轨道波函数对磁矩在z方向的分量算符是本征函数

所以

即m不仅决定了轨道角动量在z方向分量的大小，还决定了轨道磁矩在z方向分量的大小，所以m被称为（轨道）磁量子数。

自旋量子数s和自旋磁量子数

类似于l和m这一对，s和是一对。

Stern-Gerlach（斯特恩-盖拉赫）实验证明，除了轨道运动电子还有自旋运动

自旋角动量在z方向的分量和自旋磁矩在z方向的分量满足

总（角）量子数和总磁量子数

电子既有轨道角动量，又有自旋角动量，把这两个加在一起称为总角动量

**注：**j的取值不能写成，因为为整数，为半整数，取不到0

电子的总角动量在z轴的分量

总结

2.3 波函数和电子云图形

2.3.1 图和图

这两种图一般只用来表示s态分布，因为只有s态的波函数只与r有关。

图：从左至右分别为1s，2s，3s，零点数等于n-1。

图：节点数等于n-1。

2.3.2 径向分布图

对进行空间积分

令

Ddr的物理意义是在半径r和r+dr的两个球面夹层中找到电子的概率

对于主量子数为n，角量子数为l的状态，极大值峰有个，节面（原点除外）个。

2.3.3 原子轨道等值线图

球节面数：，角节面数：

图中角节面数为1，球节面数为1，所以显示的为3p轨道

以等值线图为基础，派生出几种其他图形。

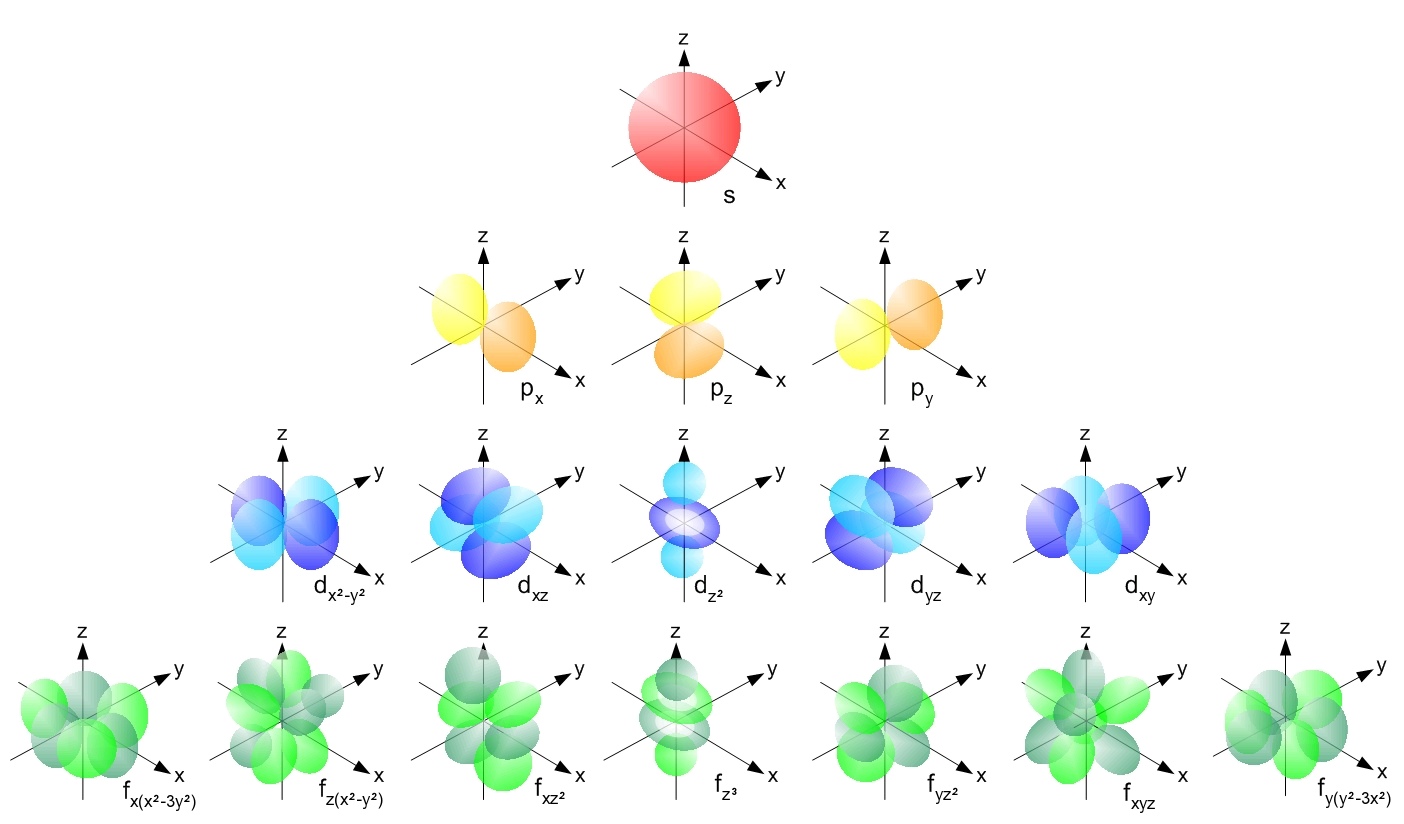
总结

本节主要内容为看懂电子云图像，能够根据电子云图像判断属于什么轨道。

径向分布图：极大值峰有个，节面（原点除外）个。

原子轨道等值线图：球节面数，角节面数

2.4 多电子原子的结构

2.4.1多电子原子的薛定谔方程及其近似解

以最简单的多电子原子氦原子为例，薛定谔方程为

[原子单位]

为了方便书写，让下表中符号一栏=1au，即等等

氦原子的薛定谔方程用原子单位（Atomic unit）表示为

同理，原子序数为Z，含n个电子的原子的薛定谔方程为

因为由i电子和j电子的坐标决定，不可能让化简成只和i或者j电子相关的一个变量，即无法分离变量，不能用解单电子原子的方法解多电子原子的薛定谔方程，只能采取近似的方法。

“暴力”近似

直接忽略掉这一项

令，分离出n个方程

再按照变数分离法，求解和

这种方法误差很大，一般不用。

中心场近似

将原子中其他电子对第i个电子的排斥作用看成球形对称的并且只与径向相关的力场。

第i个电子的势能满足

薛定谔方程为

解得

最后

[Slater规则]

(1)电子排序分组，排序按照从主量子数增大、角量子数增大；分组按照sp一组，其余单独成组

(2)外层电子对内层电子无屏蔽作用，

(3)同组电子，

(4)相邻内一组

(5)更向内组

适用于主量子数1~4轨道，其余准确性较差

自洽场法

假定第i个电子处在原子核与其他(n-1)个电子形成的平均势场中，即把原子核与其他(n-1)个电子看成一个等效电荷（类似于中心场近似），此时i电子的势能为。与中心场近似不同的是，求解这个“等效电荷”的方法为

求时，需要假设（假设的方法可以很随意，比如利用“暴力”近似解出的波函数）；求时，需要假设；求出一轮的波函数。进行下一次循环，逐渐逼近。

2.4.2 单电子原子轨道能和电子结合能

单电子原子轨道能：单电子波函数对应的能量值。

电子结合能：即第一电离能，中性原子中当其他电子均处在可能的最低能态时，某电子从指定轨道上电离所需能量的负值。可以反映电子能级的高低。

1.屏蔽效应和钻穿效应

专业定义

屏蔽效应：多电子原子中核电荷对某一电子的吸引作用，部分地被其他电子对该电子的排斥作用相抵消的效应。

钻穿效应：多电子原子中每个电子为避开其他电子的屏蔽，其电子云钻到进核区而感受到更大核电荷作用的效应。

通俗理解

屏蔽效应和钻穿效应强调的重点不同。

屏蔽效应强调客观事实，也就是说一个电子因为其他电子的客观存在，它状态发生了改变。

钻穿效应强调主观能动性，也就是说一个电子通过一定手段阻止这种改变的发生。

举例：

在一个学习氛围浓厚、老师讲课十分有趣的课堂中，班内所有的学生都非常向往能够坐在前排，这样就可以近距离与老师交流互动。由于课堂内有多名学生，座位靠后的学生因为前排同学的存在，导致了自己不能与老师近距离互动，这就是“屏蔽效应”。后面的学生也想近距离听到老师讲课呀，于是他们就搬着自己的板凳做到了前排的位置，但由于自己的桌子还在后排，过一会自己还得回到自己的座位上，这样学生通过“把凳子搬到前排”这个行为，实现了自己可以在一段时间内和老师交流互动。这种学生通过某种手段，改变了自己只能在后排与老师交流互动的状态称为“钻穿效应”。最后学生可以和老师交流互动的机会，可以由学生桌子的位置（学生大部分时间所处的位置）和学生凳子搬到的位置（学生小部分时间所处的位置）所决定。

在一个原子中，老师就是带正电的原子核，学生就是带负电的电子，学生想要坐到前排的动力就是库仑力，教室内的桌子就是能级的主峰，凳子就是能级的小峰，把凳子搬到前排这个行为就是电子在靠近核电荷处有个小峰。